LeetCode 4. 使数组唯一的最小增量

摘要：

题目

给定整数数组 A，每次 move 操作将会选择任意 A[i]，并将其递增 1。
返回使 A 中的每个值都是唯一的最少操作次数。

示例1：

输入：[1,2,2]
输出：1
解释：经过一次 move 操作，数组将变为 [1, 2, 3]。

示例2：

输入：[3,2,1,2,1,7]
输出：6
解释：经过 6 次 move 操作，数组将变为 [3, 4, 1, 2, 5, 7]。
可以看出 5 次或 5 次以下的 move 操作是不能让数组的每个值唯一的。

提示：

$0 <= A.length <= 40000$

$0 <= A[i] < 40000$

先排序再遍历

首先将数组进行排序，然后从左到右遍历数组：

如果当前元素大于上一个元素，保持不变；
如果当前元素小于等于上一个元素，就需要增加当前元素，直到大于上一个元素。
例如输入 [3, 2, 1, 2, 1, 7]，排序后为[1, 1, 2, 2, 3, 7]。遍历数组的过程如下图所示：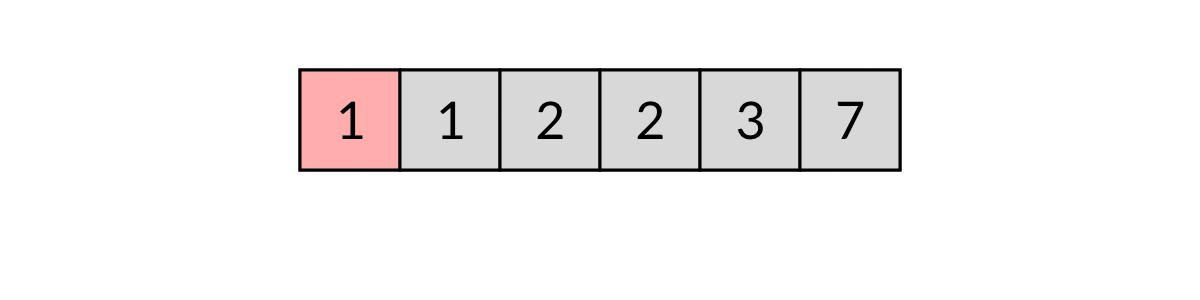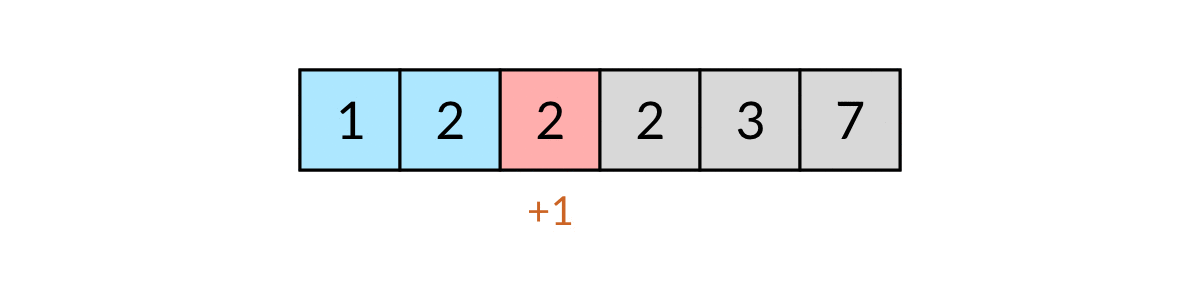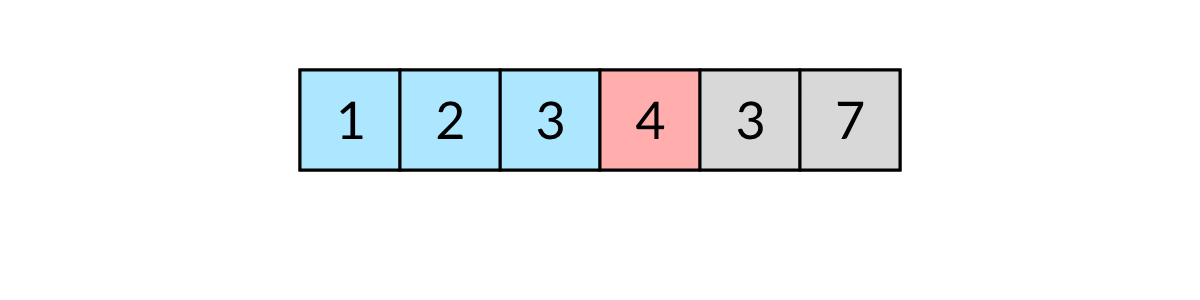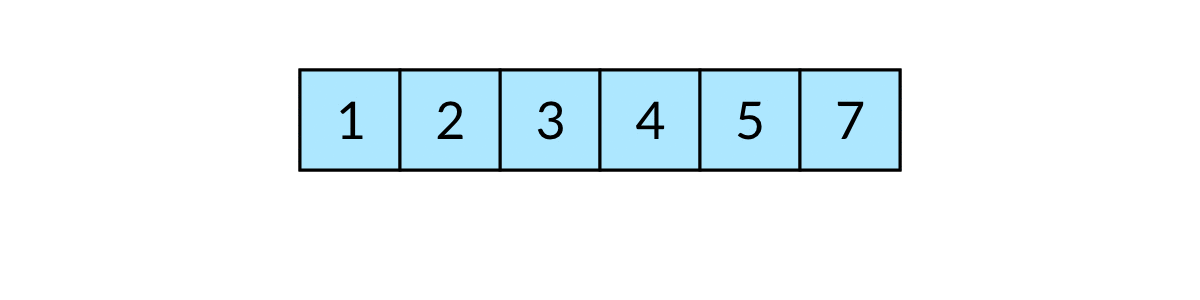

写成代码，只需要用一个变量保存当前的最大值即可。题解代码：

Java

class Solution {
    //排序再遍历计数，最基础的计算方法
    public static int minIncrementForUnique(int[] A) {
        //特殊情况
        if (A == null)
            return 0;
        else if (A.length <= 1)
            return 0;

        int res = 0;
        Arrays.sort(A);
        //下个数不比当前数大，则计算下个数需要加的次数res，同时
        //由于每次move操作+1，故下个数+res刚好大于当前数
        //注意此时数组排序会被打乱，不能认为判断条件仅是相等情况.
        //另外，注意边界，最多判定到lengh - 2位置
        for (int i = 0; i < A.length - 1; i++){
            if (A[i+1] <= A[i]){
                res += (A[i] - A[i+1] + 1);
                A[i+1] += (A[i] - A[i+1] + 1);
            }
        }
        return res;
    }
}

构建计数数组

上面方法中，排序需要 $O(nlogn)$ 的时间，比较昂贵。我们尝试不进行排序的方法。

例如输入 [3, 2, 1, 2, 1, 7]，计数之后有两个 1 和两个 2。我们先看最小的数，两个 1 重复了，需要有一个增加到 2，这样 2 的数量变成了三个。在三个 2 中，又有两个需要增加到 3，然后又出现了两个 3 …… 以此类推，可以计算出需要增加的次数。

我们可以用 map（如 C++ 的 unordered_map，Java 的 HashMap）来做计数。不过既然题目中说明了整数的范围在 $0$ 到 $40000$ 之间，我们不妨直接用一个大小为 $40000$ 的数组做计数。

需要注意的是，虽然整数的范围是 $0$ 到 $40000$，但是由于整数还会因为增加而变大，超出 $40000$ 的范围。例如极端的情况：所有数都是 $39999$。所以需要对整数中最大的数单独处理。代码如下：

Java

class Solution1 {
    //计数数组（有序）
    public static int minIncrementForUnique(int[] A) {
        if (A == null)
            return 0;
        else if (A.length <= 1)
            return 0;
        //核心思想，是record数组的构建
        //record数组是有序数组，index表示A数组中的值，value表示A数组中数值出现的次数
        int[] record = new int[40000];
        int max= A[0];
        for (int a : A) {
            record[a]++;
            max = Math.max(max, a);
        }
        //A数组中最大数max一定在record数组最后面，等下要加以特殊处理
        int res = 0;
        for (int i = 0; i < max; i++) {
            if (record[i] > 1) {
                res += (record[i] -1);
                //record是动态的
                //如果当前位置数值>1，说明下个位置数值会增加当前位置数值-1
                record[i+1] += (record[i] -1);
            }
        }
        //A数组最大值max在record数组中特殊处理
        //max位于record右边界的情况
        if (record[max] > 1) { //否则不用担心越界
            int plus = record[max] - 1; //首项（尾项1）
            res += (plus + 1) * plus / 2;
        }
        return res;
    }
}

原题链接： LeetCode 4. 使数组唯一的最小增量