LeetCode 999. 可以被一步捕获的棋子数

摘要：
简单的模拟过程题目。

题目：

在一个 $8 \times 8$ 的棋盘上，有一个白色的车（Rook），用字符 'R' 表示。棋盘上还可能存在空方块，白色的象（Bishop）以及黑色的卒（pawn），分别用字符 '.'，'B' 和 'p' 表示。不难看出，大写字符表示的是白棋，小写字符表示的是黑棋。

车按国际象棋中的规则移动。东，西，南，北四个基本方向任选其一，然后一直向选定的方向移动，直到满足下列四个条件之一：

• 棋手选择主动停下来。
• 棋子因到达棋盘的边缘而停下。
• 棋子移动到某一方格来捕获位于该方格上敌方（黑色）的卒，停在该方格内。
• 车不能进入/越过已经放有其他友方棋子（白色的象）的方格，停在友方棋子前。

你现在可以控制车移动一次，请你统计有多少敌方的卒处于你的捕获范围内（即，可以被一步捕获的棋子数）。

示例1：

输入：

{
    {'.','.','.','.','.','.','.','.'},
    {'.','.','.','p','.','.','.','.'},
    {'.','.','.','R','.','.','.','p'},
    {'.','.','.','.','.','.','.','.'},
    {'.','.','.','.','.','.','.','.'},
    {'.','.','.','p','.','.','.','.'},
    {'.','.','.','.','.','.','.','.'},
    {'.','.','.','.','.','.','.','.'},
};

输出： 3
解释： 在本例中，车能够捕获所有的卒

示例2：

输入：

{
    {'.','.','.','.','.','.','.','.'},
    {'.','p','p','p','p','p','.','.'},
    {'.','p','p','B','p','p','.','.'},
    {'.','p','B','R','B','p','.','.'},
    {'.','p','p','B','p','p','.','.'},
    {'.','p','p','p','p','p','.','.'},
    {'.','.','.','.','.','.','.','.'},
    {'.','.','.','.','.','.','.','.'},
};

输出： 0
解释： 象阻止了车捕获任何卒

示例3：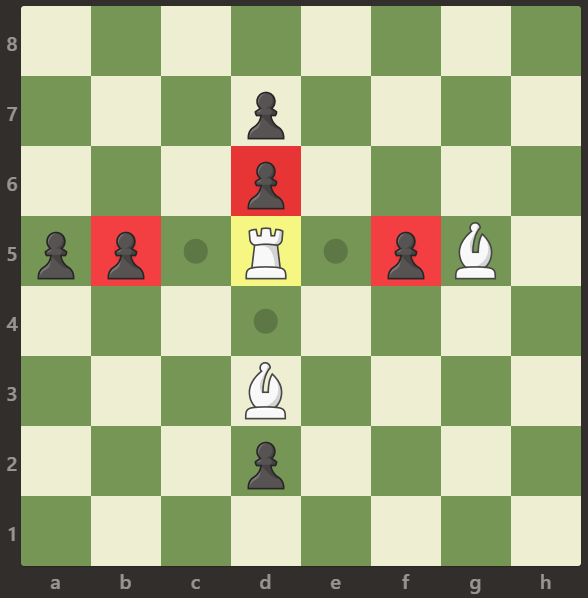

输入：

{
    {'.','.','.','.','.','.','.','.'},
    {'.','.','.','p','.','.','.','.'},
    {'.','.','.','p','.','.','.','.'},
    {'p','p','.','R','.','p','B','.'},
    {'.','.','.','.','.','.','.','.'},
    {'.','.','.','B','.','.','.','.'},
    {'.','.','.','p','.','.','.','.'},
    {'.','.','.','.','.','.','.','.'},
}

输出： 3
解释： 车可以捕获位置 b5，d6 和 f5 的卒

提示：

1. board.length == board[i].length == 8
2. board[i][j] 可以是 'R'，'.'，'B' 或 'p'
3. 只有一个格子上存在 board[i][j] == 'R'

---

题目所求即白车 rock(R) 一次移动击杀小卒 pawn(p) 所有可能的情况。
读懂题意后，先找白车 R ，以 R 为起点，分别往四个方向寻找 p。
注意可能会遇到 Bishop(B) ，表示此路不通。另注意范围。

普通解法

• Java

class Solution {
    public static int numRookCaptures(char[][] board) {
        int res = 0;
        for (int i = 0; i < board.length; i++) {
            for (int j= 0; j < board[0].length; j++) {
                if (board[i][j] == 'R') {
                    int y = i, x = j;
                    //纵上
                    while (--i >= 0) {
                        if (board[i][j] == 'B') break;
                        else if (board[i][j] == 'p') {
                            res++;
                            break;
                        }
                    }
                    //纵下
                    i = y; //i归位
                    while (++i <= 7) {
                        if (board[i][j] == 'B') break;
                        else if (board[i][j] == 'p') {
                            res++;
                            break;
                        }
                    }
                    //横左
                    i = y;//i归位
                    while (--j >= 0) {
                        if (board[i][j] == 'B') break;
                        else if (board[i][j] == 'p') {
                            res++;
                            break;
                        }
                    }
                    //横右
                    j = x;//j归位
                    while (++j <=7) {
                        if (board[i][j] == 'B') break;
                        else if (board[i][j] == 'p') {
                            res++;
                            break;
                        }
                    }
                }
            }
        }
        return res;
    }
}

二维方向数组

依然是先找到R，定义方向数组[[-1, 0], [1, 0], [0, 1], [0, -1]]，循环该方向数组可表示依次走一个方向。
走其中某个方向时，用i, j分别加方向数组即可完成行走动作，注意在行走时要判断棋盘范围。

• C++
• Java

class Solution {
public:
    static constexpr int dr[4] = {-1, 0, 1, 0}, dc[4] = {0, 1, 0, -1};

    int R, C;
    int res = 0;

    void dfs(vector<vector<char>> &board, int i, int j, int k) {
        if (i < 0 || i > R - 1 || j < 0 || j > C - 1 || board[i][j] == 'B') {
            return;
        }
        if (board[i][j] == 'p') {
            res++;
            return;
        }
        dfs(board, i + dr[k], j + dc[k], k);
    }

    int numRookCaptures(vector<vector<char>>& board) {
        this->R = board.size(), this->C = board[0].size();
        for (int i = 0; i < R; i++) {
            for (int j = 0; j < C; j++) {
                if (board[i][j] == 'R') {
                    for (int k = 0; k < 4; k++) {
                        dfs(board, i, j, k);
                    }
                    return res;
                }
            }
        }
        return res;
    }
};

class Solution {

    public int numRookCaptures(char[][] board) {
        // 因为题目已经明确给出 board.length == board[i].length == 8，所以不做输入检查
        // 定义方向数组，可以认为是四个方向向量，在棋盘问题上是常见的做法
        int[][] directions = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};

        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 8; j++) {
                
                if (board[i][j] == 'R') {
                    int res = 0;
                    for (int[] direction : directions) {
                        if (burnout(board, i, j, direction)) {
                            res++;
                        }
                    }
                    return res;
                }
            }
        }
        // 代码不会走到这里，返回 0 或者抛出异常均可
        return 0;
    }

    /**
     * burnout 横冲直撞的意思（来自欧路词典）
     *
     * @param board     输入棋盘
     * @param x         当前白象位置的横坐标
     * @param y         当前白象位置的纵坐标
     * @param direction 方向向量
     * @return 消灭一个 p，就返回 true
     */
    private boolean burnout(char[][] board, int x, int y, int[] direction) {
        int i = x;
        int j = y;
        while (inArea(i, j)) {
            // 是友军，路被堵死，直接返回
            if (board[i][j] == 'B') {
                break;
            }

            // 是敌军，拿下一血（不知道一血这个词是不是这么用的）
            if (board[i][j] == 'p') {
                return true;
            }

            i += direction[0];
            j += direction[1];
        }
        return false;
    }

    /**
     * @param i 当前位置横坐标
     * @param j 当前位置纵坐标
     * @return 是否在棋盘有效范围内
     */
    private boolean inArea(int i, int j) {
        return i >= 0 && i < 8 && j >= 0 && j < 8;
    }
}

原题链接： LeetCode 999. 可以被一步捕获的棋子数