摘要:
二叉树的对称性。
题目
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 $[1,2,2,3,4,4,3]$ 是对称的。
1
2
3
4
5
| 1
/ \
2 2
/ \ / \
3 4 4 3
|
但是下面这个 $[1,2,2,null,3,null,3]$ 则不是镜像对称的:
进阶:
你可以运用递归和迭代两种方法解决这个问题吗?
二叉树定义:
注意判断二叉树的对称性无法使用中序遍历结果的对称性来判断。
比如给定一颗二叉树:$[5,4,1,null,1,null,4,2,null,2,null]$
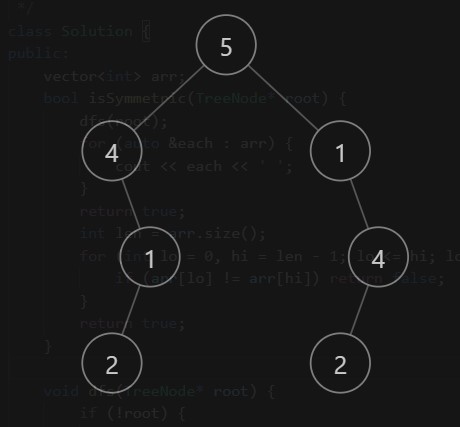
中序遍历结果是:
$[4, 2, 1, 5, 1, 2, 4]$
DFS
我们可以将对整个二叉树是否对称的判断拆分成对若干节点对是否对称的判断。这是递归思想。
具体地,从 root 节点的左右孩子节点开始,进行一次判断。条件满足的话,再深入到 node1 的 left 与 node2 的 right、node1 的 right 与 node2 的 left。依次递归下去。
注意回溯的情况,当 node1 和 node2 都为空时,即该节点对为对称的且为末端节点,return true。
不满足上面条件时,当 node1 和 node2 有一个为空或者node1.val != node2.val时,必然非对称,return false。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
bool res = true;
bool isSymmetric(TreeNode* root) {
if (!root) return res;
dfs(root->left, root->right);
return res;
}
void dfs(TreeNode* node1, TreeNode* node2) {
if (!node1 && !node2) return;
if ((!node1 && node2) || (node1 && !node2)) {
res = false;
return;
}
if (node1->val != node2->val) {
res = false;
return;
}
dfs(node1->left, node2->right);
dfs(node1->right, node2->left);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) return true;
return cmp(root.left, root.right);
}
private boolean cmp(TreeNode node1, TreeNode node2) {
if (node1 == null && node2 == null) return true;
else if (node1 == null || node2 == null || node1.val != node2.val) return false;
else return cmp(node1.left, node2.right) && cmp(node1.right, node2.left);
}
}
|
迭代
我们可以引入一个队列,迭代判断所有节点对。
第一代 poll root 节点的左右孩子节点,判断节点状态。
往后每一代(如果有的话)保留了上一代判断条件得出的信息,poll 出两个节点,再进行下一个判断。
一次又一次,迭代地进行判断。只要中间出现了一个不满足对称的情况:
node1 == null || node2 == null || node1.val != node2.val,直接return false。
当所有节点入队出队迭代判断完毕均为出现非对称情况,那么可以认为二叉树是对称的。
注意到 null 节点的情况,队列应该使用 LinkedList 而非 ArrayDeque ——前者支持 null 元素,而后者不支持。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public:
static constexpr int N = 1010;
pair<TreeNode*,TreeNode*> q[N];
int hh = 0, tt = -1;
bool isSymmetric(TreeNode* root) {
if (!root) return true;
q[++tt] = {root->left, root->right};
for (; tt >= hh; ++hh) {
TreeNode* node1 = q[hh].first;
TreeNode* node2 = q[hh].second;
if (!node1 && !node2) continue;
if ((!node1 && node2) || (node1 && !node2)) return false;
if (node1->val != node2->val) return false;
q[++tt] = {node1->left, node2->right};
q[++tt] = {node1->right, node2->left};
}
return true;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) return true;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root.left);
queue.offer(root.right);
while (!queue.isEmpty()) {
TreeNode node1 = queue.poll();
TreeNode node2 = queue.poll();
if (node1 == null && node2 == null) continue;
if (node1 == null || node2 == null || node1.val != node2.val) return false;
queue.offer(node1.left);
queue.offer(node2.right);
queue.offer(node1.right);
queue.offer(node2.left);
}
return true;
}
}
|
