VIRTUALS

the virtual labs for the virtuals

0%

LeetCode 149. 直线上最多的点数

Posted on Edited on In , ,

摘要：
主要是考虑从哪个角度入手暴搜。

题目

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

示例1:

0x0

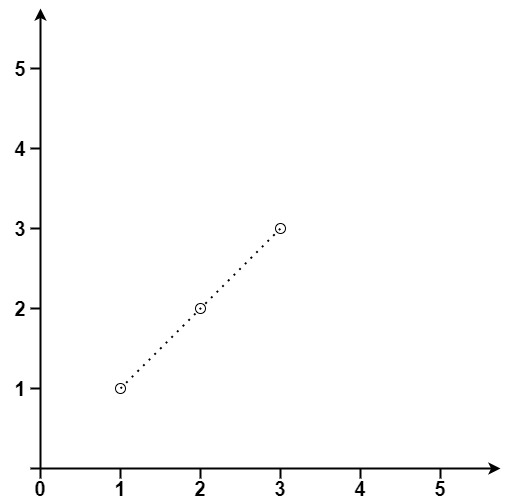
输入：points = [[1,1],[2,2],[3,3]]
输出：3

示例2:

0x1

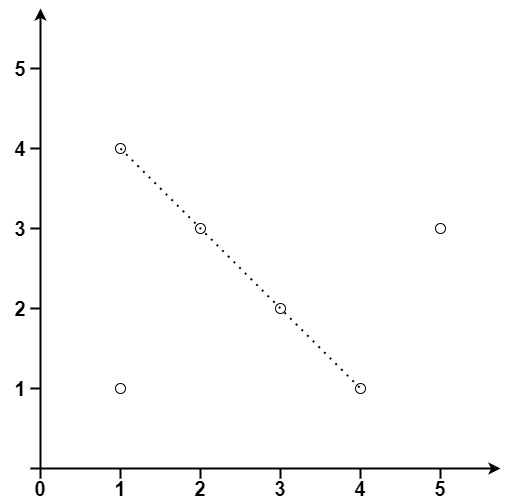
输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

提示：

  • $1 <= points.length <= 300$
  • $points[i].length == 2$
  • $-10^4 <= xi, yi <= 10^4$
  • $points$ 中的所有点 互不相同

暴搜

对于某一个点，把它看成中心点，平面上会有无穷多条直线经过它。对于一个中心点，剩余点的每个点都和它构成一条直线。我们统计剩余点和中心点构成直线的数量。

注意剩余点和中心点垂直的情况，此时可以用一个额外的变量来统计和中心点垂直的点的数量。
注意相同点的情况，即剩余点和中心点重合，虽然题目条件说明所有点互不相同，但是这里依旧考虑这一情况。
注意本题精度要求较高，计算斜率使用 long double 变量。
如果精度要求更高，可以考虑用分数来存放斜率，这时候需要求分子分母最大公约数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/*
 * 2021-6-24 17:54:50
 * @Author: etoa
 */
static const auto shutdown = [](){
    cin.tie(nullptr)->sync_with_stdio(false);
    return nullptr;
}();

class Solution {
public:
    int maxPoints(vector<vector<int>>& points) {
        int len = points.size();
        int res = 0;
        for (int i = 0; i < len; i++) {
            unordered_map<long double, int> cnt;

            int center = 0, vertical = 0;
            long double ratio = 0;

            for (int j = 0; j < len; j++) {
                if (points[j] == points[i]) center++;   // 至少包含一个中心点 points[i]
                else if (points[j][0] == points[i][0]) vertical++;
                else {
                    ratio = (long double)(points[j][1] - points[i][1]) / (points[j][0] - points[i][0]);
                    cnt[ratio]++;
                }
            }
            // 垂线和斜线数量取较大者
            int mxratio = vertical;
            for (auto [key, value] : cnt) {
                mxratio = max(mxratio, value);
            }
            res = max(res, mxratio + center);
        }
        return res;
    }
};

原题链接： LeetCode 149. 直线上最多的点数