【LeetCode周赛247】B LeetCode 1914. 循环轮转矩阵

摘要：
一道模拟过程的题目，不难，但是有点繁琐。

题目

给你一个大小为 $m \times n$ 的整数矩阵 $grid$ ，其中 $m$ 和 $n$ 都是偶数；另给你一个整数 $k$ 。

矩阵由若干层组成，如下图所示，每种颜色代表一层：

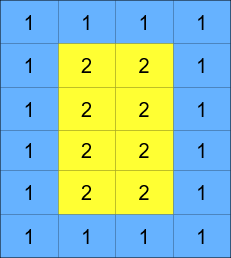
矩阵的循环轮转是通过分别循环轮转矩阵中的每一层完成的。在对某一层进行一次循环旋转操作时，层中的每一个元素将会取代其 逆时针 方向的相邻元素。轮转示例如下：

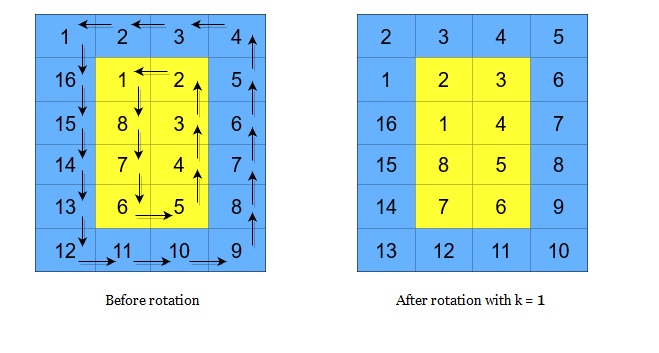
返回执行 $k$ 次循环轮转操作后的矩阵。

示例 1：

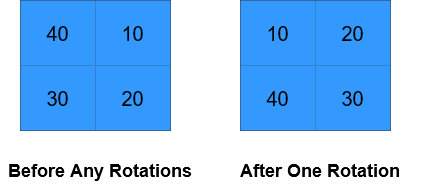
输入：grid = [[40,10],[30,20]], k = 1
输出：[[10,20],[40,30]]
解释：上图展示了矩阵在执行循环轮转操作时每一步的状态。

示例 2：

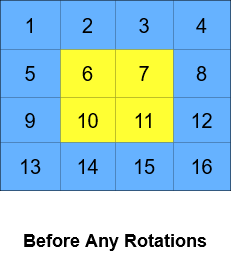
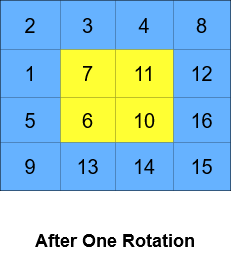
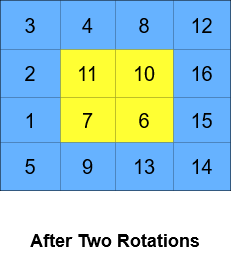
输入：grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
输出：[[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
解释：上图展示了矩阵在执行循环轮转操作时每一步的状态。

模拟

将每一层放到一个队列中，再计算出每一层的每一位对应轮转 $k$ 次后在队列中的什么位置。
将每一层分为 $4$ 次分别处理入队，分别是上右下左，依次是行不变列增加；行增加列不变；行不变列减小；行减小列减小。
另外注意不能数组原地替换，因为前面被替换的数原本包含着最后的要替换的数的数。所以需要额外维护一个同样大小的数组。

class Solution {
public:
    vector<vector<int>> rotateGrid(vector<vector<int>>& grid, int k) {
        int R = grid.size(), C = grid[0].size();
        vector<vector<int>> res(R, vector<int>(C, 0));
        for (int mxr = R, mxc = C, begin = 0; mxr > 0 && mxc > 0; mxr -= 2, mxc -= 2, ++begin) { // 逐层将坐标放入数组中
            vector<pair<int, int> > queue;
            int r = begin, c = begin;
            for (int i = 0; i < mxc - 1; i++) queue.emplace_back(r, ++c);
            for (int i = 0; i < mxr - 1; i++) queue.emplace_back(++r, c);
            for (int i = 0; i < mxc - 1; i++) queue.emplace_back(r, --c);
            for (int i = 0; i < mxr - 1; i++) queue.emplace_back(--r, c);
            //for (auto &each : queue) cout << grid[each.first][each.second] << " ";
            //cout << endl;
            int len = queue.size();
            for (int i = 0; i < len; i++) {
                int t = (i + k) % len;
                res[queue[i].first][queue[i].second] = grid[queue[t].first][queue[t].second];
            }
        }
        return res;
    }
};

模拟 + DFS

我的思路是先确定一共需要进行多少层轮转，对于每一层的每一次轮转写进行一次深搜，一共 $k$ 次，注意 $k$ 需要对一层的总数取模。

核心在于如何对指定层进行一次轮转。

深搜从每一层的左上角开始，所以我们要确定每一层的第一个数坐标。
深搜过程中到达拐点处需要改变搜索方向，所以我们需要知道每一层的长和宽。
另外我们需要对搜索过的格子进行计数，以便判断递归终止。

class Solution {
public:
    static constexpr int dr[4] = {1, 0, -1, 0}, dc[4] = {0, 1, 0, -1};
    int R, C;
    vector<vector<int>> rotateGrid(vector<vector<int>>& grid, int k) {
        R = grid.size(), C = grid[0].size();
        int level = min(R, C) >> 1;
        //cout << level << endl;
        //return res;
        for (int i = 0, mod = 0; i < level; i++) {
            mod = 2 * (R - i * 2) + 2 * (C - i * 2) - 4;
            //cout << mod << endl;
            int t = k % mod;
            rotation(grid, i, t, mod, R - i * 2, C - i * 2);
        }
        return grid;
    }

    void inline rotation(vector<vector<int>> &g, int level, int k, int mod, int mxr, int mxc) {
        pair<int, int> start = {0 + level * 1, 0 + level * 1};
        for (int direction = 0; k--; direction = 0) {
            dfs(0, g, start, start, 0, mod, mxr, mxc, direction);
        }
    }   

    void dfs(int value, vector<vector<int>> &g, pair<int, int> &start, pair<int, int> pos, int cnt, int &mod, int &mxr, int &mxc, int &direction) {
        //cout << pos.first << ',' << pos.second << "," << cnt << ',' << mod <<endl;
        if (cnt == mod) {
            g[pos.first][pos.second] = value;
            return;
        }
        int nevalue = g[pos.first][pos.second];
        g[pos.first][pos.second] = value;
        if ((pos.first == start.first + mxr - 1 && pos.second == start.second) || (pos.first == start.first + mxr - 1 && pos.second == start.second + mxc - 1) || (pos.first == start.first && pos.second == start.second + mxc - 1)) {
            direction++;
        }
        int ner = pos.first + dr[direction], nec = pos.second + dc[direction];
        dfs(nevalue, g, start, {ner, nec}, cnt + 1, mod, mxr, mxc, direction);
        return;
    }
};

原题链接： LeetCode 1914. 循环轮转矩阵